Comment étudier scientifiquement un phénomène extraordinaire ?
Résumé
Lors de la Fête de la science, en octobre 2006 et 2007, l’Observatoire zététique a présenté une animation aux scolaires et au grand public, en deux parties. La première partie vise à améliorer le protocole d’une expérience de recherche d’eau volontairement mal conçue, pour faire comprendre quelques règles simples à respecter pour avoir une démarche rigoureuse (double aveugle, randomisation). La deuxième partie explique le principe de l’analyse statistique des résultats obtenus à une telle expérience, en ébauchant un test d’hypothèse. Cet article présente cette animation dans le détail.
I. Présentation
1. La Fête de la science
La Fête de la science est une manifestation annuelle organisée en octobre partout en France par différents acteurs. À Lyon, le Centre de culture scientifique, technique et industrielle (CCSTI) du Rhône fédère les actions menées et organise le Village départemental des sciences sur le campus de la Doua de l’Université Claude Bernard Lyon 1. Il s’agit d’un vaste hall où une trentaine d’exposants disposent chacun d’un stand. Le Village départemental ouvre ses portes le jeudi à midi, reçoit les groupes de scolaires ayant réservé leur passage le jeudi après-midi et le vendredi toute la journée, puis tout public les samedi et dimanche après-midi.
En 2006 et 2007, l’Observatoire zététique a tenu un stand au Village départemental des sciences. Il y a proposé, pour les scolaires, une animation d’environ trois quarts d’heure mise au point en 2006 et reprise en 2007, en plus de nouveautés. Cette animation a été également utilisée hors de la Fête de la science, lors d’interventions diverses dans des établissements scolaires.
2. Participation de l’Observatoire zététique
Le stand de l’Observatoire zététique a pour titre « Esprit (critique), es-tu là ? », reprenant la question de Henri Broch1, qui évoque à la fois le thème de l’esprit critique et celui de l’occultisme. L’objectif de l’Observatoire zététique, en participant à cette manifestation, est de sensibiliser le public à la démarche scientifique en montrant, à travers quelques règles simples, qu’il s’agit d’une démarche de bon sens et qu’elle n’est pas réservée aux scientifiques professionnels, mais qu’au contraire chacun peut se l’approprier sans connaissances spécifiques préalables.
L’intérêt d’utiliser, dans ce cadre, le « paranormal » comme support de discours, est qu’il s’agit d’un thème accrocheur : dans ce domaine, le public se pose des questions auxquelles il ne sait souvent pas comment répondre proprement. Ceci est conforme à l’un des objectifs de l’Observatoire zététique : la diffusion de la démarche scientifique et sa vulgarisation. Le thème utilisé est la recherche d’eau, dans la mesure où on peut réaliser des expériences faciles à mettre en oeuvre dans le cadre de la Fête de la science.
3. L’animation
L’animation dont il sera question ici comporte deux parties, chacune utilisable indépendamment de l’autre dans des contextes variés. La première partie invite le public à construire un protocole expérimental rigoureux pour mettre en évidence un phénomène étrange (trouver de l’eau par un « pouvoir » spécial). La deuxième partie s’intéresse à l’analyse statistique des résultats d’une expérience de ce genre et aux conclusions qu’on est en droit d’en tirer.
Nous allons décrire l’animation telle que nous l’avons élaborée en octobre 2006 et telle qu’elle a été présentée au public depuis par plusieurs membres de l’Observatoire zététique. Nous expliquerons également quel discours tenir et pourquoi nous avons fait tel ou tel choix de présentation. Cette animation a été faite, au moins partiellement, à environ 700 personnes, allant du public scolaire de niveau CM1 aux familles comprenant enfants, parents et grands-parents, par petits groupes allant jusqu’à trente personnes lors de la Fête de la science, mais aussi à une assemblée de 80 lycéens et enseignants.
4. Motivation de cet article
Comme dans l’ensemble le public ayant participé à l’animation semble avoir été satisfait et intéressé, il ne nous paraît pas inutile de la faire partager. En outre, cette animation est le résultat de plusieurs années d’essais et de réflexions qui ont permis une nette amélioration de la clarté du discours que nous tenons : nous pensons donc que les choix pédagogiques que nous avons fait ne vont pas de soi et qu’il est bon de les exposer.
Néanmoins, sur un plan didactique, aucune mesure d’efficacité n’a été faite. Nous restons donc très modestes sur la portée d’une telle animation et sur sa qualité. Toute suggestion d’amélioration est la bienvenue.
II. Première partie : mise en place d’un protocole rigoureux
Cette partie nécessite deux personnes au moins, que l’on désignera dans la suite comme « l’animateur » et « le comparse ». L’essentiel du discours sera tenu par l’animateur, afin de ne pas brouiller l’écoute en multipliant les orateurs, mais le comparse tiendra une part importante dans l’élaboration des expériences.
1. Introduction
Description
L’animateur et le comparse se présentent comme ce qu’ils sont vraiment (des membres d’une association s’intéressant à l’étrange de manière scientifique).
L’animateur brandit un pendule et interroge le public sur ce qu’il sait de la radiesthésie. Le mot de radiesthésie est parfois inconnu, en revanche le pendule évoque systématiquement l’hypnose. L’animateur définit donc la radiesthésie comme une méthode utilisée par certains pour trouver des choses cachées (de l’eau souterraine, des métaux enfouis, des personnes disparues…). Le professeur Tournesol, qui utilise son pendule2 pour retrouver un trésor, est souvent connu.
L’animateur propose alors de réaliser une expérience pour savoir s’il a la capacité de découvrir de l’eau. Il annonce même qu’il n’utilisera pas de pendule et range celui-ci quelque part, loin de la zone de travail. Pendant ce temps, le comparse prépare l’expérience.
Commentaires
La présentation doit être la plus honnête possible ; il est très important d’être clair sur ses motivations et de ne pas mentir sur sa qualité, en se prétendant radiesthésiste par exemple. La radiesthésie peut être évoquée, parce qu’il est fréquent que le public sache ce que c’est et fasse le lien entre ce qu’il va voir et les sourciers. Autant prendre les devants, donc, mais sans pour autant insister. On n’est pas là pour dire « la radiesthésie, ça marche », ou « la radiesthésie, ça ne marche pas », mais pour montrer comment il faudrait faire pour savoir si « ça marche » ou pas, dans un cas bien précis. Il faut bien insister sur ce point, afin de ne pas laisser de malentendu sur les conclusions finales. Du coup, on ne laisse pas de prise aux deux remarques suivantes, parfois faites par le public.
- « Vous avez montré que vous n’avez pas de don radiesthésique, mais ça ne veut pas dire que la radiesthésie, ça ne marche pas » : remarque faite souvent par des personnes ayant pratiqué ou vu pratiquer la radiesthésie. Cette affirmation est presque3 exacte, mais elle est sans objet puisque personne n’a jamais rien dit dans cette animation sur la validité de la radiesthésie.
- « De toutes façons, tout le monde sait bien que ça ne marche pas » : remarque faite souvent par les « incrédules ». Cette affirmation est aussi sans objet.
Il est très important de ne pas laisser repartir le public avec l’idée qu’il a vu des expériences réfutant la radiesthésie. Il faut donc bien préciser qu’on ne fait pas de radiesthésie et toujours dédramatiser les choses en gardant un ton léger et un oeil complice faisant comprendre que l’expérience n’est que le prétexte à autre chose.
C’est pourquoi il ne faut pas se servir de pendule. Il faut même le ranger loin et pas dans sa poche, parce que certains enfants peuvent penser qu’il y a un effet dû au pendule qui fonctionne même dans la poche.
2. Première expérience
Description
Le comparse dispose devant une planche contenant dix cases numérotées de A à J dix gobelets et en remplit cinq. Il se dirige ensuite vers un tableau où il prépare la notation des affirmations de l’animateur en expliquant le formalisme utilisé (par exemple O pour « oui, il y a de l’eau », N pour « non »). Il note donc les dix lettres en ligne et se prépare à noter ce que dit l’animateur.

Yeux ouverts, l’animateur passe sa main à cinq centimètres au-dessus des gobelets et annonce ses résultats « oui » ou « non » (ou « plein » ou « vide », etc.). Il fait taire les ricanements et les remarques intempestives s’il y en a en demandant le silence pour sa concentration.
Une fois les dix gobelets prédits, le comparse effectue la vérification et note le score obtenu par l’animateur.
Commentaires
Évidemment, l’animateur obtient 10/10, qu’il ait un don de radiesthésiste ou non. Rien ne l’empêche, à ce stade, de voir les gobelets, qui ne sont pas recouverts par quoi que ce soit.
Il est important, pour la seconde expérience, que cinq gobelets soient remplis : on verra plus loin pourquoi.
3. Discussions sur la première expérience
Description
Le public proteste sur le fait que, l’animateur pouvant voir les gobelets, ce score de 10/10 est « trop facile ». Même si l’animateur prétend ne pas avoir utilisé la vue, certains dans le public ne sont pas convaincus. L’animateur insiste alors sur la distinction entre observation (de l’eau a été trouvée) et explication (ou hypothèse, ou théorie). Tout le monde est d’accord sur l’observation, mais il y a des explications concurrentes : la vue et le « pouvoir » allégué sont les principales.
Le public est conduit à en proposer d’autres : généralement, la sensation de froid qu’engendrerait la présence d’eau dans le gobelet est une explication avancée par les plus petits, qui prétendent même parfois ressentir cette sensation de froid.
On écrit donc sur le tableau un diagramme séparant l’observation de l’explication et détaillant les différentes hypothèses en présence. On pourrait en rester là, mais il faudrait faire un choix en se passant d’informations supplémentaires, ce qui conduirait à choisir l’hypothèse la plus simple (ici, la vue). On rappelle que l’on veut vérifier une et une seule explication : le mystérieux pouvoir. On cherche donc à éliminer les deux principales concurrentes : la vue et la sensation de froid.
On introduit donc la notion d’expérience en aveugle. On insiste sur le fait que ce n’est pas seulement la vue qui doit être supprimée, mais aussi la sensation de froid : être aveugle, dans ce sens-là, ce n’est pas seulement ne pas voir, mais c’est ne pas savoir directement à l’aide d’un moyen sensoriel autre que celui que l’on cherche à mettre en évidence.
Commentaires
Il est rare qu’à ce stade, l’explication concurrente du hasard soit avancée. On peut donc la proposer à ce moment-là ou après les résultats de la deuxième expérience.
Il ne faut pas hésiter à noter au tableau le schéma de la démarche effectuée, ainsi que les mots importants (« aveugle », par exemple).
4. Préparation de la deuxième expérience
Description
Pour réaliser une expérience en aveugle, le public propose généralement de bander les yeux de l’animateur. Celui-ci, alléguant que ce ne serait pas pratique parce qu’alors quelqu’un devrait lui tenir la main au-dessus des gobelets, propose plutôt un dispositif constitué de dix boîtes de conserve vides fixées sur une planche et permettant de recouvrir l’ensemble des gobelets, chacun sous une boîte. Il précise que l’on se place dans le cas d’un « pouvoir » qui fonctionnerait encore à travers le métal.
Il place ce dispositif sur les gobelets, mais doit s’interrompre immédiatement car le public proteste qu’il faut changer les verres de place par rapport à la première expérience. L’animateur acquiesce, change les verres de place et veut replacer le cache, mais le public proteste à nouveau qu’il ne faut pas que ce soit l’animateur qui mélange les gobelets. Il acquiesce évidemment et laisse le comparse déplacer les gobelets sous ses yeux. Le public proteste une fois de plus, dit que l’animateur ne doit rien voir et finit par le faire sortir en déléguant quelqu’un pour le surveiller.

Commentaires
Outre dans le fait qu’effectivement, il n’y a besoin de personne pour tenir la main de l’animateur, l’intérêt du dispositif des boîtes de conserve réside dans sa polyvalence, puisqu’il sera réutilisé pour la deuxième partie de l’animation.
À ce stade, rester ostensiblement présent lors de la préparation de l’expérience conduit le public à s’impliquer dans l’expérience : on s’est déjà moqué de lui une fois, on ne s’en moquera pas deux fois.
5. Deuxième expérience (facultative)
Description
L’animateur étant sorti, le comparse déplace les gobelets ou propose au public de déplacer les gobelets, mais en tous cas garde le contrôle de l’expérience. Cela lui permet, en ayant l’air de placer les gobelets n’importe comment, de les placer d’une manière prédéfinie avec l’animateur. Le comparse replace le cache, demande à faire revenir l’animateur et se place en position de noter ses prédictions.
L’animateur revient, passe sa main sur chaque boîte et annonce ses prédictions, que le comparse note. On soulève le cache, note l’adéquation et annonce un score : 10/10.
En général, le public est un peu embêté mais pas convaincu. L’animateur fait valoir que pourtant, cette fois, l’expérience était faite en aveugle et qu’il n’avait pas moyen de connaître les résultats puisque les gobelets avaient été placés par décision du public dans un ordre qu’il ne pouvait pas connaître.
Le public finit alors par avouer qu’en fait, c’est plus ou moins le comparse qui a placé les verres… On refait donc l’expérience.
Commentaires
Cette deuxième étape est facultative, parce qu’il arrive fréquemment que le public ne laisse pas au comparse le soin de placer les gobelets.
Pour que l’animateur, qui n’a pas assisté à la mise en place des verres, sache qui les a placés, on peut convenir d’un code visuel simple avec le comparse : par exemple, si le comparse est en position de noter les résultats sur le tableau, c’est que c’est lui qui a placé les verres. Sinon, le comparse est placé dans le public, face à l’animateur.
6. Troisième expérience (deuxième si la précédente n’a pas eu lieu)
Description
L’animateur étant sorti, le public déplace les gobelets. Le comparse donne des instructions pour que le cache, en étant placé, ne renverse pas les gobelets et surveille la manipulation. Il se place dans le public, en vue de l’animateur.
L’animateur revient, passe sa main sur chaque boîte et annonce ses prédictions, qu’une personne du public note. On soulève le cache, note l’adéquation et annonce le score : 10/10.
Commentaires
Le comparse doit être présent à cette étape pour pouvoir donner des indications à l’animateur. Il se donne donc un rôle de superviseur de l’expérience et généralement personne n’essaye, à ce stade, de le faire sortir.
L’animateur trouve ici grâce à une communication secrète entre le comparse et lui. Cela peut être un code visuel (sur la position des pieds du comparse, par exemple, qui peuvent être bien visibles pour l’animateur puisque celui-ci est penché sur les gobelets), un code verbal (plus compliqué à mettre en place) ou simplement une communication en aparté, si la vigilance du public n’est pas bonne.
7. Discussions : randomisation et double aveugle
Description
Si les gobelets ont été placés avec un motif particulier (par exemple alternance plein-vide, ou bien cinq pleins, puis cinq vides), il y a lieu de discuter de la randomisation. De l’anglais random signifiant « aléatoire », la randomisation est le fait de tirer au sort, pour chaque gobelet, s’il sera plein ou vide. En effet, jusqu’à présent et sauf exceptions, le public n’a pas modifié le nombre total de verres remplis (cinq), ce qui est en soi une information pour l’animateur. On a d’ailleurs pris soin de ne pas mettre d’eau à disposition du public jusque là.
Il faut donc bien faire comprendre que les gobelets n’ont pas été placés là par hasard, mais suite à une décision d’un être humain. Pour montrer qu’on ne peut pas faire confiance à l’être humain pour être un bon générateur de hasard, on peut faire, au passage, l’expérience rapide de faire choisir au hasard un chiffre entre 1 et 9 au public : il devrait y avoir très peu de 9 ou de 1 et beaucoup de 7 normalement.4
Ensuite, il faut amener le public à soupçonner le comparse. Il faut aussi jeter le doute sur le fait qu’une personne du public puisse être de mêche avec l’animateur. Surtout, il faut faire remarquer que le public pouvait donner inconsciemment des informations à l’animateur (et souvent il le fait, par des hochements de tête ou des ricanements). On ajoute, sur le tableau, à côté de l’explication « pouvoir », les explications « tricherie » et « informations inconscientes ».
Pour éliminer ces deux explications supplémentaires, on amène donc le public à construire une expérience en double aveugle : non seulement l’animateur sera aveugle, mais l’équipe qui note les résultats autour de lui le sera aussi.
Commentaires
Il est arrivé plusieurs fois qu’à ce stade, le public dispose cinq gobelets pleins à la suite, puis cinq gobelets vides. Même lorsqu’il ne le fait pas, il est intéressant de citer ce fait, parce qu’il arrive que quelqu’un dise alors qu’il avait pensé à cette disposition, pensant que l’animateur ne pourrait jamais la deviner. Une occasion de plus d’insister sur le fait qu’il faut s’en remettre au meilleur hasard possible, c’est-à-dire pas fabriqué par un être humain.
Lors de la discussion sur la randomisation, il arrive que certains dans le public comprennent qu’on a une chance sur 1024 de trouver tout juste par hasard. On peut faire remarquer que ce n’est pas vrai parce que tant que les gobelets sont placés suite à une décision humaine et non suite à un tirage, toutes les configurations ne sont pas équiprobables.
8. Dernière expérience
Description
Cette dernière expérience doit être clairement et entièrement préparée à l’avance. On insiste à cette occasion sur la nécessité absolue de préparer le protocole complètement avant de réaliser l’expérience et de s’y tenir absolument.
Une équipe, contenant l’animateur, doit sortir : cette équipe sera, par la suite, appelée « équipe de contrôle ». Le reste du public formera l’« équipe de remplissage » : son rôle est de placer les gobelets en tirant à pile ou face (ou avec un dé) le remplissage. L’équipe de remplissage replace le cache et avertit l’équipe de contrôle, par un moyen convenu à l’avance et ne pouvant transmettre aucune information, que l’expérience est prête. L’équipe de remplissage sort sans croiser l’équipe de contrôle qui revient. L’équipe de contrôle note les prédictions de l’animateur et fait rentrer l’équipe de remplissage. On enlève le cache et note le score : n/10.
Commentaires
Cette expérience est plus facile à décrire qu’à réaliser, puisqu’il faut un moyen pour que les deux équipes ne se rencontrent pas, mais puissent s’avertir. Cela dépend de la configuration des lieux. En pratique, il est rarement possible de faire cette expérience de manière bien contrôlée lorsqu’il y a un public nombreux. Peu importe au fond, puisqu’on ne cherche pas réellement à tester les capacités radiesthésiques de l’animateur, mais à montrer le principe de réalisation d’une bonne expérience. On peut d’ailleurs, avant de dévoiler le résultat, revenir sur les conditions de l’expérience et discuter de la rigueur : était-on bien en aveugle ? Normalement oui. En double aveugle ? Souvent, pas vraiment. L’expérience était-elle randomisée ? En principe oui, même si un tirage à pile ou face n’est pas vraiment satisfaisant (avec de l’entraînement, on peut faire sortir ce que l’on veut).
9. Appréciation du résultat et conclusions
Description
Quel que soit le résultat n/10 obtenu, l’animateur tente, le sourire en coin, de le faire passer pour extraordinaire. S’il est en-dessous de 5 (résultat moyen par hasard), il dira « c’est mieux que rien, quand même », s’il est au-dessus, il dira « c’est mieux que par hasard ».
Il peut aussi arguer qu’il a fait 10/10 aux deux (ou trois) premières expériences, donc « en tout ça fait 24/30, c’est quand même très bien ». L’occasion de montrer qu’on ne peut en aucun cas assembler des données qui ne sont pas obtenues dans les mêmes conditions.
C’est le moment, si ce n’est pas déjà fait, de rajouter à la liste des hypothèses sur le tableau, dont seule n’a pas été biffée l’explication du « pouvoir », l’hypothèse du « hasard », du « coup de bol ». Le public convient en général facilement que tous les scores sont possibles par hasard, même 10/10, le score maximal.5 Pour illustrer cela, on peut prendre l’exemple du loto : s’il était impossible de trouver tout juste par hasard, seuls les personnes ayant des capacités spéciales (précognition…) gagneraient le gros lot.
Alors quel score serait considéré comme extraordinaire, comme montrant autre chose qu’un résultat obtenu par hasard ? Certains votent pour 7 ou plus, d’autres pour 8, d’autres disent qu’aucun score de cette expérience, même 10/10, ne les convaincrait, et qu’il faut refaire l’expérience.
À ceux qui pensent qu’il faut refaire l’expérience, on demande à partir de combien d’essais ils seraient convaincus. Trente, cent, etc. Mais on fait remarquer que si tous les scores peuvent être obtenus par hasard, même 100/100 peut l’être, donc on est coincé : l’animateur n’arrivera jamais à montrer son pouvoir s’il en a un, parce qu’on lui opposera sans cesse qu’il a pu l’obtenir par hasard.
Comme tout le monde n’est pas d’accord puisque tout le monde n’a pas la même appréciation de ce qui est extraordinaire ou pas, on montre ainsi la nécessité d’obtenir un critère objectif. Il s’agit de chiffrer l’extraordinaire, ce qui passe par un problème de probabilités et de statistiques : c’est l’objet de la deuxième partie de l’animation.
Commentaires
Lors du commentaire du dernier résultat obtenu, il ne faut pas se prendre au sérieux lorsqu’on avance des arguments relevant de la mauvaise foi, toujours afin de dédramatiser les choses et de bien rappeler que l’on n’est pas là pour tester les capacités radiesthésiques de l’animateur, mais pour discuter de ce que serait une bonne expérience.
C’est le moment de bien repréciser cela, de dire que si quelqu’un a le pouvoir de trouver l’eau ainsi, on devrait accepter qu’il fasse une expérience pour le mettre en évidence. L’expérience doit être préparée proprement à l’avance, y compris dans ses issues possibles.
Cela sera vu dans la deuxième partie sur le traitement statistique des résultats. Si on n’a pas le loisir de faire cette deuxième partie de l’animation, on peut soit en résumer les conclusions, soit laisser la question en suspens et récapituler les quelques principes expérimentaux (aveugle, randomisation, double aveugle) en ajoutant celui de la nécessité d’une réplication suffisante et de l’analyse statistique des résultats.
Dernière remarque : on a passé sous silence un aspect important des choses : la nécessité d’une validation objective des résultats. En effet, ici, la question ne se posait pas vraiment puisque le gobelet soit contenait de l’eau, soit n’en contenait pas. Le résultat (vrai ou faux) était donc incontestable.6 La question de la validation objective peut être évoquée : pour une expérience de voyance où l’on se contenterait de descriptions passe-partout de l’image qu’on est censé percevoir, il faudrait évaluer si la description est conforme à l’image-cible et cela se ferait à l’aide de critères subjectifs, dépendants du juge chargé d’évaluer les résultats. Mettre en place une validation objective des résultats signifie faire en sorte que l’issue de l’expérience (vrai ou faux) ne repose que sur des critères objectifs et non sur l’appréciation d’un être humain.
III. Deuxième partie : analyse statistique des résultats
Cette deuxième partie est indépendante de la première ; elle peut être proposée en complément pour répondre à la question de l’analyse des résultats qui se pose à la fin de la première partie ou utilisée seule. Il n’y a plus aucune tricherie, puisque le but ici n’est pas d’élaborer un bon protocole, mais d’analyser le score obtenu à l’issue de l’expérience.
1. Expérience
Description
Tout le monde est invité à participer à l’expérience.
On réutilise le système planche-boîtes de conserve de la première partie, ainsi que dix jetons en caoutchouc présentant sur une face une croix, sur l’autre un rond. On place un jeton dans chaque boîte, et on ferme l’ensemble des boîtes à l’aide de la planche (l’ensemble est maintenu fermé par des aimants). En secouant le dispositif ainsi formé, on réalise dix tirages à pile ou face (ou plutôt dix tirages à croix ou rond) en même temps. L’ensemble est posé sur la table, boîtes en l’air, de sorte que le tirage est fait mais invisible.

On a bien ici une expérience en aveugle (quiconque fait une prédiction ne peut pas savoir directement quel tirage est sorti), en double aveugle (en fait, personne ne peut savoir) et randomisée (sauf si les jetons ne sont pas parfaitement équilibrés). On distribue à chaque personne du public une grille dans laquelle, à la ligne « prédiction », il faut inscrire, pour chaque boîte de A à J, une croix ou un rond. On demande au public d’admettre que l’on cherche à tester ses capacités de clairvoyance sur l’issue du tirage dans chaque boîte.
Commentaires
On pourrait, pour cette analyse statistique, poursuivre l’expérience de recherche d’eau en faisant participer tout le monde. Mais ce serait plus délicat à mettre en oeuvre, parce qu’il faudrait faire sortir le public pendant les tirages au sort vide/plein pour chaque gobelet. De plus, il y a un côté amusant à ces dix tirages aléatoires faits en même temps : il faut secouer, ça fait du bruit, etc. On peut faire remarquer que c’est exactement, du point de vue du hasard et indépendamment de toute prétention paranormale, la même expérience : dix tirages à une chance sur deux chacun.
Ici encore, il ne faut pas trop insister sur le « don de clairvoyance », pour rester le plus léger possible et le plus en dehors du paranormal possible : on ne veut pas tester la voyance mais illustrer un questionnement mathématique.
2. Discussion sur les résultats
Une fois que chacun a fait sa prédiction sur la grille de réponse, il faut se mettre d’accord sur les conclusions que l’on tirera, quelle que soit l’issue de l’expérience. Il faut évidemment fixer les choses avant de noter les résultats, afin de savoir où l’on va clairement.
La question est la suivante : si tous les scores, de 0/10 à 10/10, peuvent être obtenus par hasard, sans capacité extraordinaire, comment pourra-t-on montrer une capacité extraordinaire à coup sûr ? La réponse est claire : on ne pourra jamais. À coup sûr, ce n’est pas possible. En revanche, c’est possible en minimisant les risques de se tromper.
Se tromper, cela peut signifier deux choses :
- conclure que l’expérience ne montre rien d’extraordinaire alors que la personne testée a réellement une capacité extraordinaire ;
- conclure que la personne testée a une capacité extraordinaire alors que le résultat a été obtenu par hasard.
Comme l’hypothèse « le résultat est obtenu par hasard » est plus banale que l’hypothèse « le hasard seul ne peut pas expliquer ce résultat, il y a autre chose », on choisit de privilégier la première (qu’on nommera aussi l’hypothèse banale7) et de demander à l’autre hypothèse de faire ses preuves.
On va donc chercher à minimiser le risque de conclure indûment à la capacité extraordinaire.
Pour cela, il faut savoir quels scores on peut obtenir par hasard. Il n’est pas question d’expliquer comment faire les calculs quel que soit le public, mais on peut établir avec le public que le score moyen est de 5/10 et que la probabilité d’obtenir un score de k/10 diminue plus on s’éloigne de cette valeur moyenne.8
Puisqu’il s’agit de fixer un score au-delà duquel on considérera que le résultat est extraordinaire, il faut calculer les probabilités d’obtenir k ou plus. On peut prévoir un tableau ou un poster qui les montre :
| score k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P(k ou plus) (en %) | 100 | 99,9 | 98,9 | 94,5 | 82,8 | 62,3 | 37,7 | 17,2 | 5,5 | 1,1 | 0,1 |
Il faut lire les choses ainsi : si on choisit de dire que les scores supérieurs ou égaux à 8/10 sont extraordinaires, alors on a 5,5% de chances de se tromper, puisqu’il y a 5,5% de chances pour que, si l’hypothèse banale du hasard est exacte, le score soit au moins égal à 8. Si on choisit de dire que les scores supérieurs ou égaux à 7/10 sont extraordinaires, alors on a 17,2% de chances de se tromper.
Il faut choisir un seuil au-delà duquel on ne considérera plus que le score est extraordinaire. Il faut bien faire comprendre qu’il s’agit d’un choix humain et non d’une opération automatique.
Le seuil choisi par les scientifiques est parfois de 5%, parfois de 1%, parfois moins. Plus le seuil est petit, moins on a de chances de conclure indûment à un résultat extraordinaire. La logique voulant que plus ce que l’on cherche à montrer est extraordinaire, plus on aimerait être certain de l’avoir montré, on propose au public de choisir le seuil de 1% : c’est-à-dire que si on a plus de 1% de chances d’obtenir tel résultat ou plus par hasard, alors on ne conclura pas que ce résultat est extraordinaire. On le voit, dans l’expérience présente, le seul score considéré comme extraordinaire sera 10/10.
On fixe donc clairement les choses : si quelqu’un, dans le public, a un score de 10/10, on n’expliquera pas son résultat par le simple hasard, mais on conclura qu’autre chose est responsable de son résultat.9 Pour savoir quoi, il faut procéder à d’autres expériences.
Commentaires
Il faut bien évidemment adapter le niveau du discours au public qu’on a en face de soi. Néanmoins, même des élèves de CM1 sont capables de comprendre le principe (« ne pas trop se tromper »).
Le seuil de 5% est couramment utilisé en psychologie ou en parapsychologie. On peut faire remarquer au passage que si on avait choisi un seuil de 5%, les scores extraordinaires seraient 9/10 et 10/10. Sur l’ensemble des tirages effectués, on a obtenu quelques 9/10 alors que personne, dans le public, n’avait de prétention extraordinaire. Il paraît peu raisonnable, en général, d’utiliser un seuil de 5% dans le domaine du paranormal, où les allégations, si elles sont vérifiées, remettent en question des pans entiers du savoir scientifique.
Stratégiquement, il faut faire toute la discussion sur l’analyse statistique des résultats avant de dévoiler le tirage obtenu. Ainsi, le public sera attentif au discours et non à son propre résultat.
3. Résultats et conclusions
Description
On peut révéler le tirage obtenu. Chacun le note, puis calcule son score. Si une personne a 10/10, alors on n’expliquera pas son score par le simple hasard, mais on cherchera autre chose.10

Chacun se voit remettre une balle de ping-pong, qu’il place dans une colonne transparente où, progressivement, l’histogramme des résultats se construit.

De gauche à droite : Florent Tournus, l’histogramme et Stanislas Antczak
Si le nombre de personnes ayant participé est suffisant et si l’hypothèse du hasard est bien vérifiée, l’histogramme se rapproche d’une loi binomiale, avec le score moyen, 5/10, qui est aussi le score le plus probable, et les effectifs qui diminuent à mesure qu’on s’en éloigne.
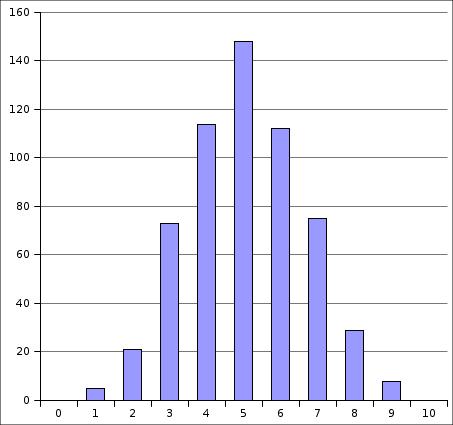
Histogramme de tous les résultats de la Fête de la science en 2006 et 2007
On peut également faire remarquer que les fluctuations par rapport à la courbe binomiale limite peuvent être importantes. Nous avions un classeur donnant les fourchettes admissibles pour chaque score en fonction du nombre total de balles.
On peut conclure en rappelant les grandes lignes de ce qui a été vu, tant au niveau du protocole expérimental qu’au niveau du principe de l’analyse statistiques. Il n’est pas inutile de rappeler qu’il faut se mettre d’accord à l’avance sur tous les points du protocole et de l’analyse, afin d’éviter les désaccords a posteriori.
Commentaires
Attention, l’histogramme peut avoir des allures bizarres sans que ce soit anormal. Il faut vraiment un grand nombre de balles pour qu’il ait l’allure d’une loi binomiale. Pour bien faire, il faut étudier l’histogramme globalement avec des tests statistiques plus élaborés, mais on n’aborde pas ce sujet avec le public.
Nous avons gardé (presque) toutes les grilles, afin de traiter les résultats après coup. Sur le moment, on n’a pas la possibilité de s’assurer que personne n’arrange les résultats (transforme un 6 en 7 par exemple) ou ne se trompe dans le relevé.
IV. Développement conclusif
L’analyse des grilles de réponses de toutes les personnes ayant participé à cette expérience en 200711 a montré très clairement que les gens ne font pas leur prédiction de manière réellement aléatoire, même lorsqu’ils pensent le faire. Ainsi, on a constaté que :
- il y a significativement plus de croix que de ronds dans les prédictions ;
- en particulier, il y a significativement beaucoup de croix prédites pour la boîte A ;
- les nombres de croix (ou de ronds) par prédiction diffèrent significativement du hasard ;
- dans les prédictions, les gens ont tendance à éviter les grandes séries de signes (croix ou ronds) identiques, bien plus que ce qui advient en moyenne par hasard.
Ce sont des mises en évidences supplémentaires du fait que l’être humain ne reproduit pas bien le hasard et que cette question mérite que l’on s’y intéresse.
Stanislas Antczak et Florent Tournus
Autres animateurs : Pierre Bienvenu, Véronique Blum, Pierre Borgnat, Géraldine Fabre et Florent Martin.
Pour toute question sur l’animation, demande de renseignement complémentaire ou suggestion d’amélioration, contacter les auteurs par l’intermédiaire de l’Observatoire zététique.
Notes
1 Henri Broch, « Le Paranormal », Points, 2001, quatrième de couverture.
2 Hergé, « Le Trésor de Rackham le Rouge », Casterman.
3 En effet, on ne peut pas dire qu’on a montré qu’on n’a pas de don de radiesthésiste, on peut dire qu’on n’a pas montré qu’on en avait un.
4 Expérience citée par Delahaye et Gauvrit, « Le hasard géométrique n’existe pas », Pour la science, mars 2006, 341. Attention, si le public est très peu nombreux, il est peu probable que le résultat soit conforme aux attentes. Pour illustrer ce mauvais choix du hasard, on peut aussi utiliser quatre boîtes identiques (boîte d’allumettes par exemple) sur les quelles on a noté « A » pour trois d’entre elles et « B » pour la quatrième et que l’on a disposé dans l’ordre ABAA. On demande au public d’en choisir une au hasard et on constate que la plupart des gens choisissent le « A » du milieu, montrant qu’il n’a pas fait un tirage au hasard mais un choix humain.
5 Plus précisément, il y a toujours eu quelqu’un dans le public pour convenir que tous les scores sont possibles par hasard, mais certains ont pu dire le contraire.
6 Et encore, il pourrait être contesté si les gobelets ne sont pas tout à fait secs.
7 Cette hypothèse, en plus d’être plus banale, est également plus simple à mathématiser : c’est la seule des deux hypothèses pour laquelle on peut calculer une loi de probabilité.
8 La probabilité d’obtenir exactement k/10 est donnée par la loi binomiale : P(k)=Cnkpk(1-p)n-k où, dans le cas qui nous occupe, n=10 et p=1/2 (une chance sur deux pour chaque tirage).
9 Ceci n’est vrai que si l’on se place du point de vue individuel de la personne qui fait la prédiction. Du point de vue de l’expérimentateur, il ne faut pas oublier que de nombreuses personnes font l’expérience et que, même si les tirages sont faits parfaitement au hasard et sans « don », le score de 10/10 peut arriver par hasard. Les prédictions étant, du point de vue statistique, indiscernables les unes des autres, pour un nombre assez grand de prédictions, un résultat individuel pourra être parfaitement normal (conforme au hasard).
10 En tenant compte des précautions développées dans la note précédente.
11 Les grilles de 2006 n’ont malheureusement pas été conservées…
